[Mason] 우리는 왜 대출을 받아 투자하는가

포트폴리오 이론의 탄생

 과거 포트폴리오는 수익과 위험이 선형적 관계를 갖는 것이 널리 알려진 사실이었다. 즉, 높은 수익을 얻기 위해서는 높은 위험을 감수해야 하는 사실이 과거 포트폴리오 이론의 기초였다. 1950년대 H. Markowitz (해리 마코위츠)가 각 자산군을 분산투자 하면 전체 포트폴리오의 위험이 선형적 관계가 아닌 비선형적 관계가 됨을 발견하였다. 이는 동일 수익 단위에서 감소된 위험을 선택할 수 있는 획기적인 이론이었다.

간단히 설명하면, w는 각 자산의 비중, 시그마는 자산간의 공분산, wT는 자산의 비중 행렬의 전치행렬이다. 마코위츠의 포트폴리오 이론 발견은 수 없이 많은 포트폴리오 선택지를 하나의 선으로 집합시켰다. 이를 효율적 투자선(Efficient-Frontier)라고 한다. 효율적 투자선은 앞서 본 포트폴리오 위험과 수익에 따라 비중이 최적화되는 집합이다.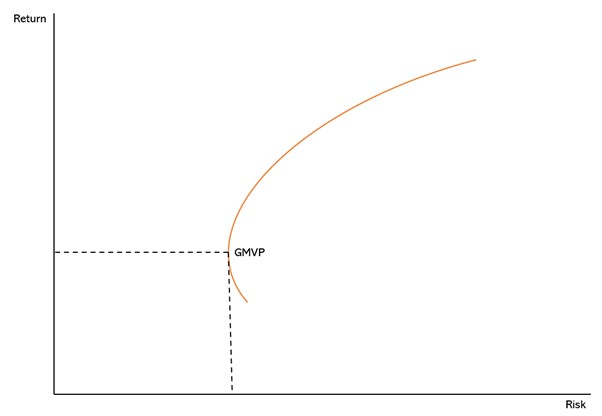




 마코위츠의 이론에 따른 최적화 방법을 Mean-Variance Optimization(평균-분산 최적화)라고 부른다. 과거, 주로 자산 수익률의 평균을 기대수익으로, 표준편차를 위험으로 설정하여 분석하여 붙여진 이름이다. 마코위츠는 이 효율적 투자선에서 꺾이는 한 점을 발견했다. 서로 다른 자산군의 비중 조합에 따라 같은 위험을 가졌지만 더 큰 수익을 얻을 수 있는 포트폴리오를 찾았고, 그에 더불어 GMVP(최소분산 포트폴리오)라 불리는 위험을 더 쪼갤 수 없는 포트폴리오 점을 발견했다. 즉, 우리는 이 최소분산을 비체계적 위험(분산투자로 쪼갤 수 있는 위험, 체계적 위험은 거시적 경제 변동 등과 같이 분산투자로 나눌 수 없는 위험임.) 이라 부르게 되었다.


포트폴리오 선택과 Separation Theorem

 마코위츠의 포트폴리오 이론은 J.P Morgan 과 같은 대형 IB 증권사에서 각광을 받았다. 하지만, 이를 실제 투자에 적용함에 있어 한 가지 의문을 갖게 되었다. 투자를 하기 위해 최소한의 목표 수익률(예를 들어, 예금금리와 같은 무위험 수익률 보다 낮은 투자 포트폴리오는 더 이상 투자라고 부르지 못한다.)을 설정하는데, 최소분산 포트폴리오보다 위에 있는 효율적 투자선에서 어떤 점을 선택해야 하는지에 대한 문제가 생겼다. 평면상의 수많은 포트폴리오 조합을 곡선으로 옮긴 것은 좋았지만 여전히 무한대의 포트폴리오 조합이 곡선 상에 존재했다.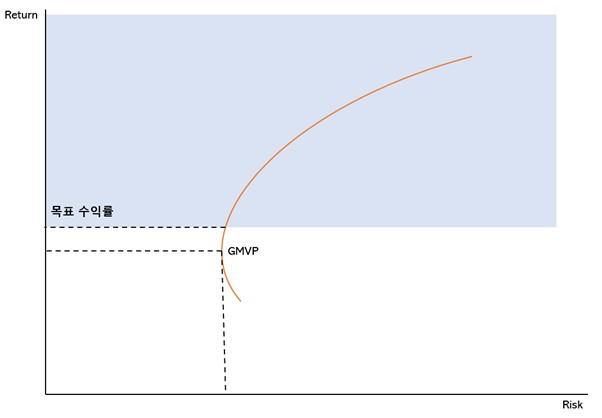




 즉, 그림의 청색 부분에 있는 효율적 투자선(주황 선)에서 포트폴리오 조합을 선택해야 하지만 그 점은 사실 무한대의 조합이 존재했다. 이를 해결하기 위해 고안된 방법이 효율적 투자선의 조합 중 수익과 위험의 비율을 최적화 시키는 것이었다.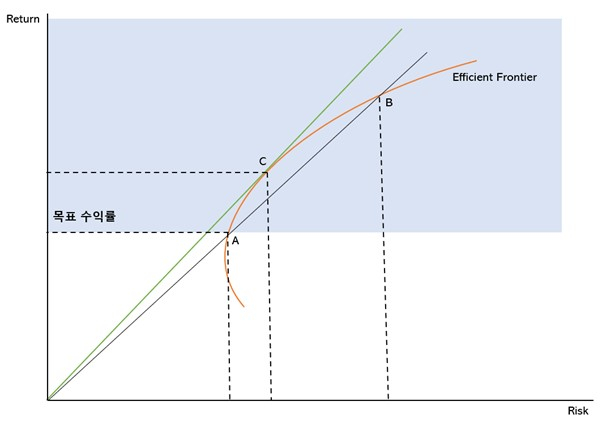


 즉, 원래 목표수익률 이상을 달성하기위한 효율적 투자선 상의 점은 A와 B 사이의 주황색 선 집단에 존재할 것이다. A는 목표수익률 달성을 위한 투자선상의 최적점이고 B는 원점에서 A점을 통하는 직선 상의 점으로 A와 수익-위험 비율이 같다. 다시 말하면, A 와 B 포트폴리오는 감수하는 위험 단위 당 얻을 수 있는 수익이 같다는 뜻이다.

 결국 앞서 말한 A 와 B 사이의 투자선에서 선택할 수 있는 최적 포트폴리오 점은 원점에서 시작되는 직선과 접하는 점이 될 것이다. 즉,  y=ax 선과 만나는 투자선의 점 중 기울기 a가 가장 큰 점이 최적 포트폴리오가 된다는 사실이다.

 이 사실이 발견된 뒤 1958년 J. Tobin (제임스 토빈)은 마코위츠 이론을 강화하는 또다른 방안을 선보였다. 누구도 고려하지 않던 Risk-free (무위험) 자산의 발견이었다. 예를 들어, 우리가 투자하는 대신 1.5% 확정금리를 받고 은행에 넣어두면 이는 위험이 없다(물론, 부도 등의 신용 위험, 환 위험 등은 제외한다.). 즉, 이 자산은 다른 자산과의 공분산이 없으며 자체로 일정한 수익이 약속된다. Tobin은 이러한 무위험 자산은 기존 위험 자산군과 상관관계가 없으며 포트폴리오 리스크에서 개별적으로 측정되야 한다는 사실을 발견했다. 이를 Separation Theorem(분리 정리)라고 한다.

 분리 정리에 따라 무위험 자산을 포트폴리오에 섞으면 다음과 같다.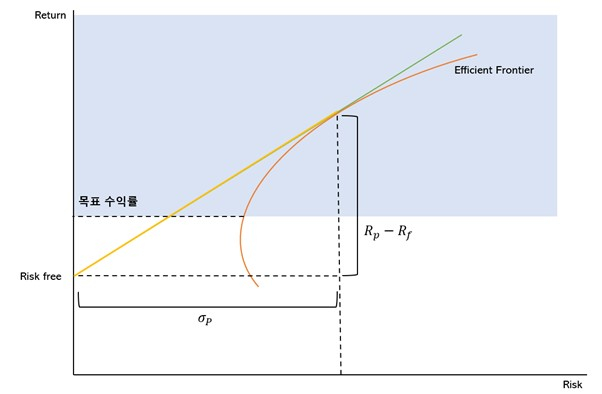






 효율적 투자선은 위험이 존재하는 자산으로 이루어져 있고 무위험 수익이 분리정리에 따라 개별적으로 포트폴리오에 기여하게 되면, 포트폴리오 위험이 없을 때, 즉 무위험 자산에 100% 투자 했을 때가 황색의 y 절편이 된다. 예로, 우리가 예금 금리 1.5%에 모든 현금을 넣고 가만히 있으면 위험은 없고 기대 수익은 1.5%인 것과 같다. 여기에 위험자산을 조금씩 섞어 포트폴리오 위험을 높이면 최적 조합 점은 황색선을 따라 우상향 한다.

 황색 선은 앞서 마코위츠가 창안한 효율적 투자선의 기울기로써 투자선과 접점을 이룬다. 이 점의 기울기는 다음과 같다.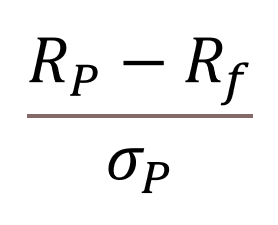






 이 기울기는 William Sharpe가 발표한 Sharpe ratio(샤프비율)과 같다는 사실을 확인할 수 있다. 즉, 무위험 자산이 섞인 포트폴리오는 샤프비율을 최대화시키는 점을 찾아야 한다. 그렇다면, 곡선으로 이루어졌던 포트폴리오는 직선으로 바뀌고, 이 직선은 무위험 자산과 위험자산의 비중 조합에 따라 수익, 위험의 선형적 행태를 보인다.

 투자자는 이 황색 선에서 스스로의 효용에 따라 포트폴리오를 선택하게 된다.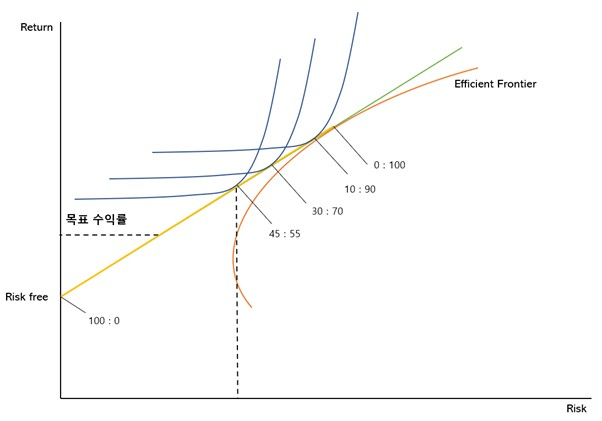






 파란 곡선을 효용함수, 즉 효용곡선이라 부르지만 간단하게 말해서 우리가 TSLA(Tesla (NASDAQ:TSLA))에 투자할 때 현금 비중을 가져가는 정도는 투자자마다 다르다. 어떤 투자자는 100%를 살 수 있고 다른 투자자는 20%를 살 수 있다. 이는 투자자가 가진 위험 선호도 즉 위험을 얼마나 감당할 수 있는지에 따라 다르다. 실제 기관 투자자는 Shortfall risk, VaR 등의 위험 척도를 이용해 이를 정량화 하지만 여기선 다루지 않겠다. 각 투자자는 황색 선에서 감당할 수 있는 리스크 라는 제한을 가지고 포트폴리오를 선택한다.

 만약 한 당신이 5년안에 집을 사기 위해 돈을 모은다고 가정해보자, 당신은 4억이 있고 5년 뒤 집값은 12억이라고 하자. 당신은 5년 뒤 이 집을 사기 위해 연간 24.57% (내부수익률을 참조) 이상의 수익을 얻어야 한다.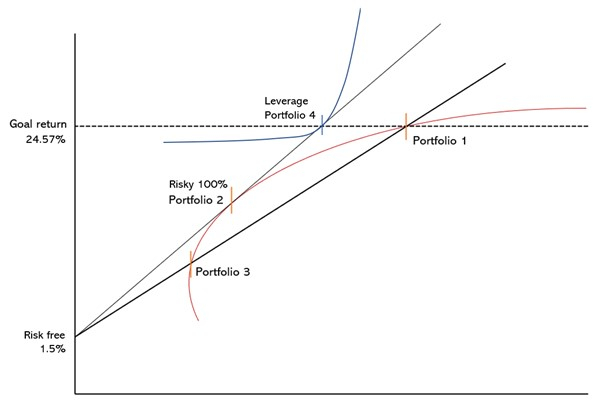






 앞서 살펴본 포트폴리오 이론에 따르면, 본래 투자선과 목표 수익률이 만나는 점 Portfolio 1 우측의 투자선에서 포트폴리오 점을 선택해야 한다. 하지만 우리는 샤프비율을 최적화 시켰고 그에 따라 좀 더 개선된 직선(Portfolio 2를 지나는 직선)을 얻게 된다. 하지만, 아직 집을 사기위한 24.57%에 도달하기에는 멀다. Tobin의 정리에 따라 무위험 자산을 이원화(개별 적용) 시켰고 최적점을 Portfolio 2 라는 위험자산 100% 지점을 찾았는데 목표달성에는 부족하다. 당신의 효용함수는 직선의 저 위에 위치해 있다. 당신은 이 포트폴리오 최적점을 얻기 위해 무위험 이자율 1.5%를 차입(실제로는 예금과 대출 금리는 다르다.)하여 대출을 받는다. 당신이 투자할 수 있는 무위험 이자율을 비용으로 지불하고 위험자산의 기대수익을 사는 것이다. 즉 당신은 대출을 받아 주식을 더 사는 전략을 택한다.

 레버리지 효과로 최적 포트폴리오 점은 직선을 따라 우상향하고 목표 수익과 일치하게 된다. 이제 당신의 효용함수에 적합한 포트폴리오를 얻을 수 있다. 무위험 자산과 위험 자산의 비율은 아마 0 : 150 혹은 그 이상이 될 것이다. 하지만, 당신이 구상한 포트폴리오 최적점은 자산의 조합으로 구현할 수 있는 모든 포트폴리오 중에 가장 뛰어나다. 심지어 대출을 받지 않은 효율적 투자선 내의 Portfolio 1보다 샤프비율이 높다. 대출을 받았지만 위험이 감소한 효과를 얻었다.

 지금까지, H.Markowitz의 Mean-Variance 모델부터 J. Tobin의 분리 정리까지 알아보았다. 21년 하반기의 포트폴리오는 이론적 모델을 통해 직접 구상해 보는 것도 좋을 것이라 생각된다.